Chapter 6: Probability

Section 6.1: Probability

Section 6.1.1: Frequentist versus Bayesian

Section 6.1.2: Definition and Axioms

Section 6.1.3: Permutations

par(cex = 1.5, mar = c(5, 5, 4, 2))
birthday <- function(k) {
    logdenom <- k * log(365) + lfactorial(365 - k) # log denominator
    lognumer <- lfactorial(365) # log numerator
    ## P(at least two have the same bday) = 1 - P(nobody has the same bday)
    pr <- 1 - exp(lognumer - logdenom) # transform back
    return(pr)
}

k <- 1:50
bday <- birthday(k)  # call the function
names(bday) <- k  # add labels
plot(k, bday, xlab = "Number of people", xlim = c(0, 50), ylim = c(0, 1),
     ylab = "Probability that at least two\n people have the same birthday")
abline(h = 0.5) # horizontal 0.5 line

bday[20:25]

##        20        21        22        23        24        25 
## 0.4114384 0.4436883 0.4756953 0.5072972 0.5383443 0.5686997

Section 6.1.4: Sampling With and Without Replacement

k <- 23 # number of people
sims <- 1000 # number of simulations
event <- 0 # counter

for (i in 1:sims) {
    days <- sample(1:365, k, replace = TRUE)
    days.unique <- unique(days) # unique birthdays
    ## if there are duplicates, the number of unique birthdays
    ## will be less than the number of birthdays, which is `k'
    if (length(days.unique) < k) {
        event <- event + 1
    }
}

## fraction of trials where at least two bdays are the same
answer <- event / sims
answer

## [1] 0.5

Section 6.1.5: Combinations

choose(84, 6)

## [1] 406481544

Section 6.2: Conditional Probability

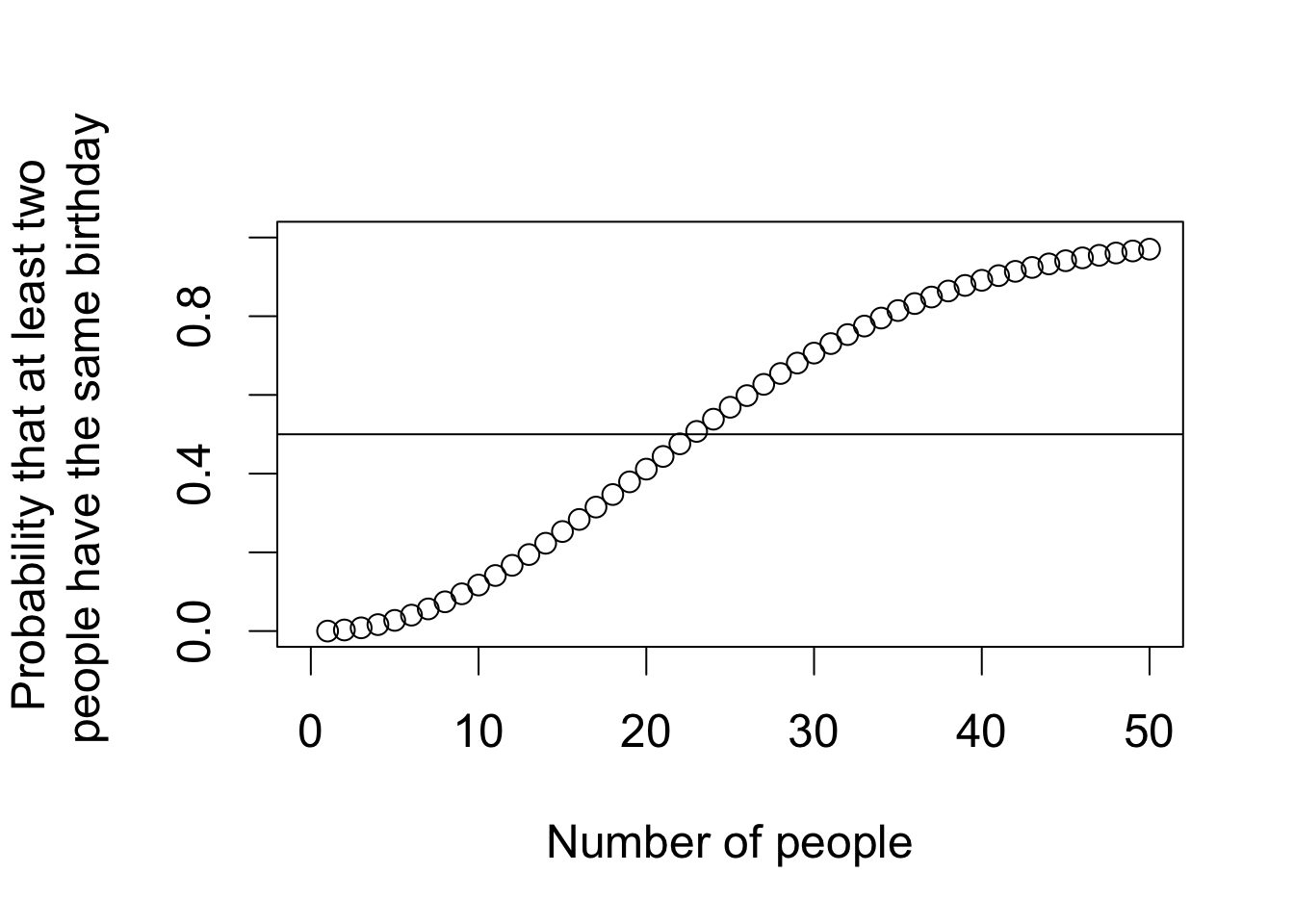
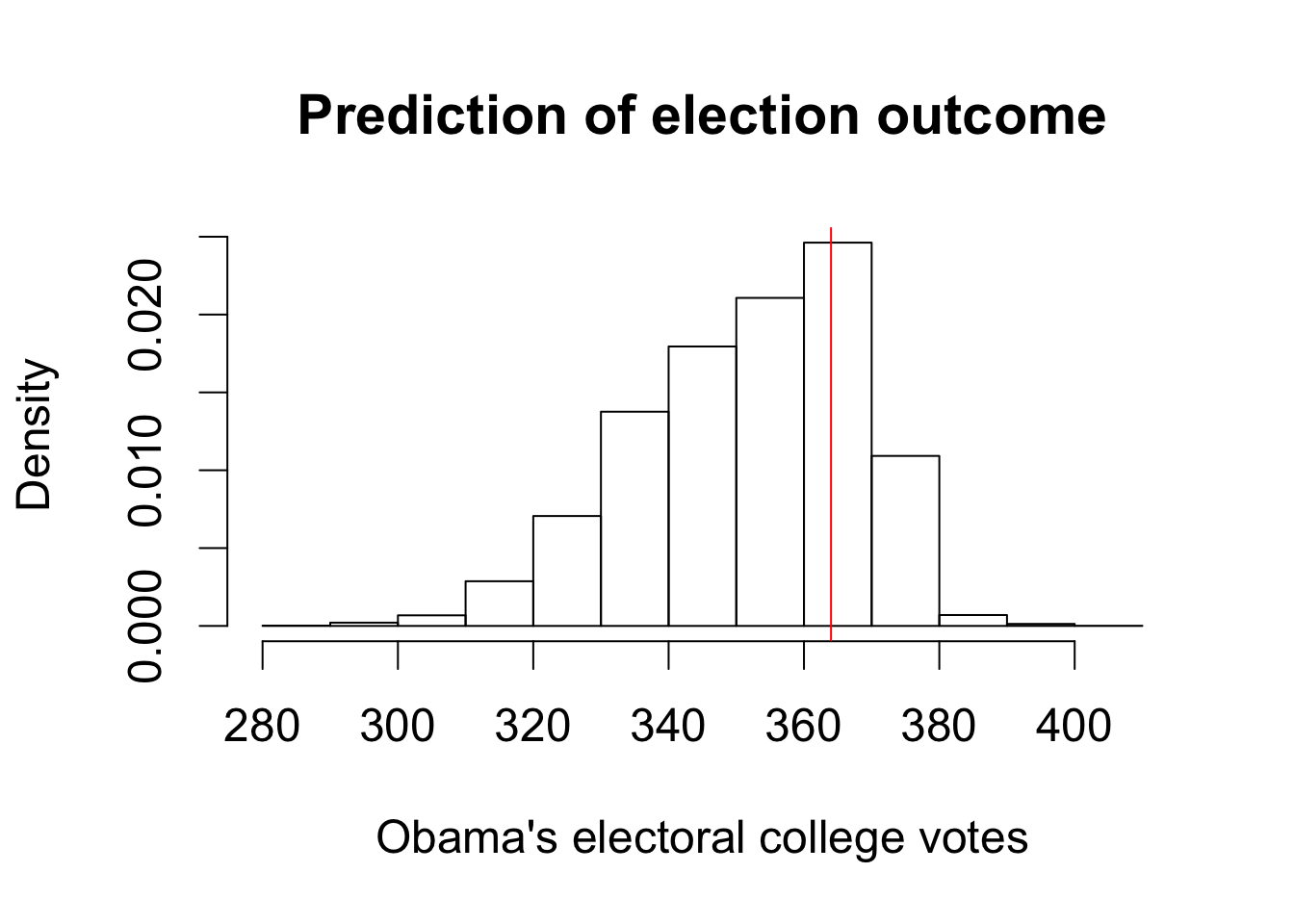
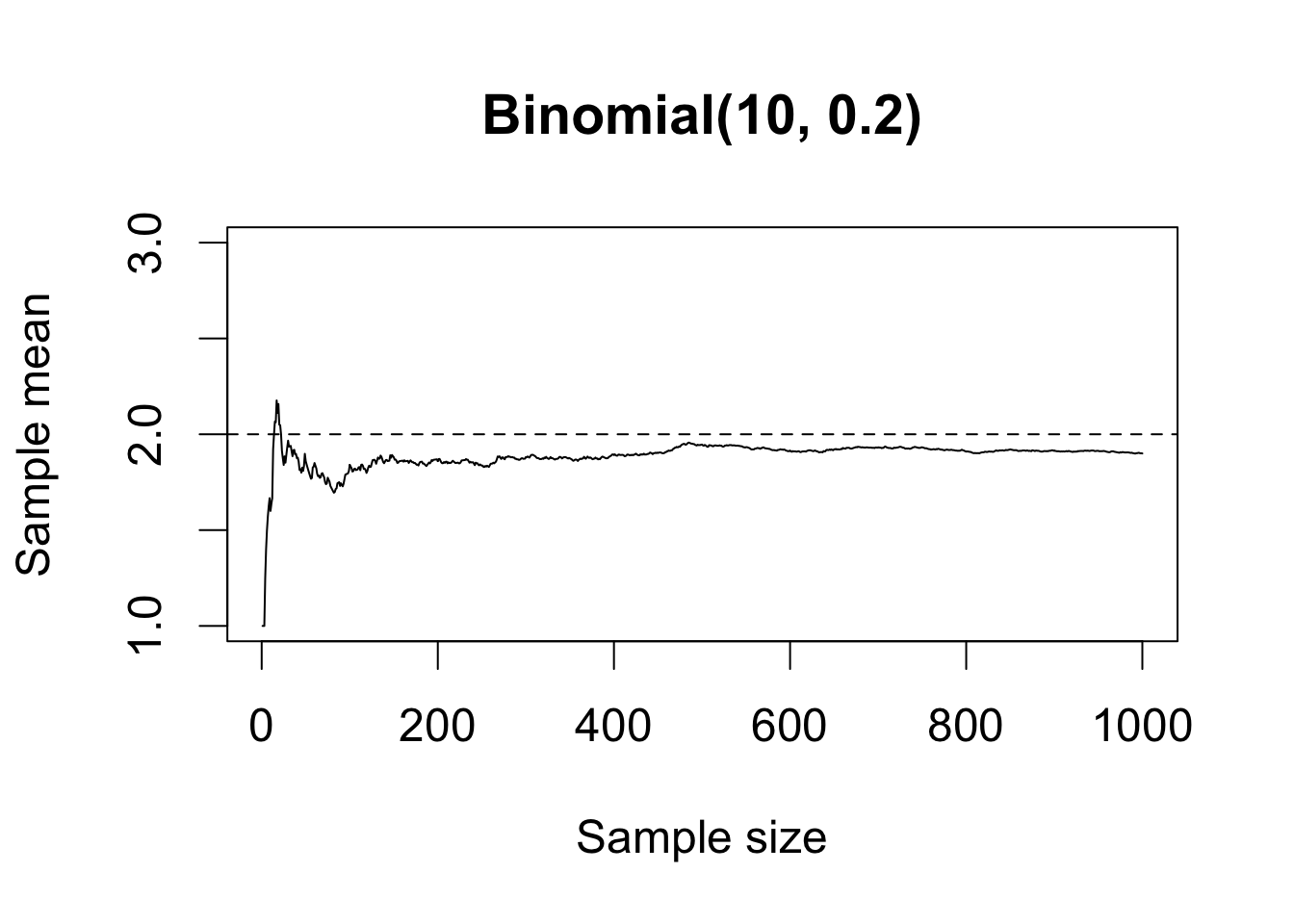
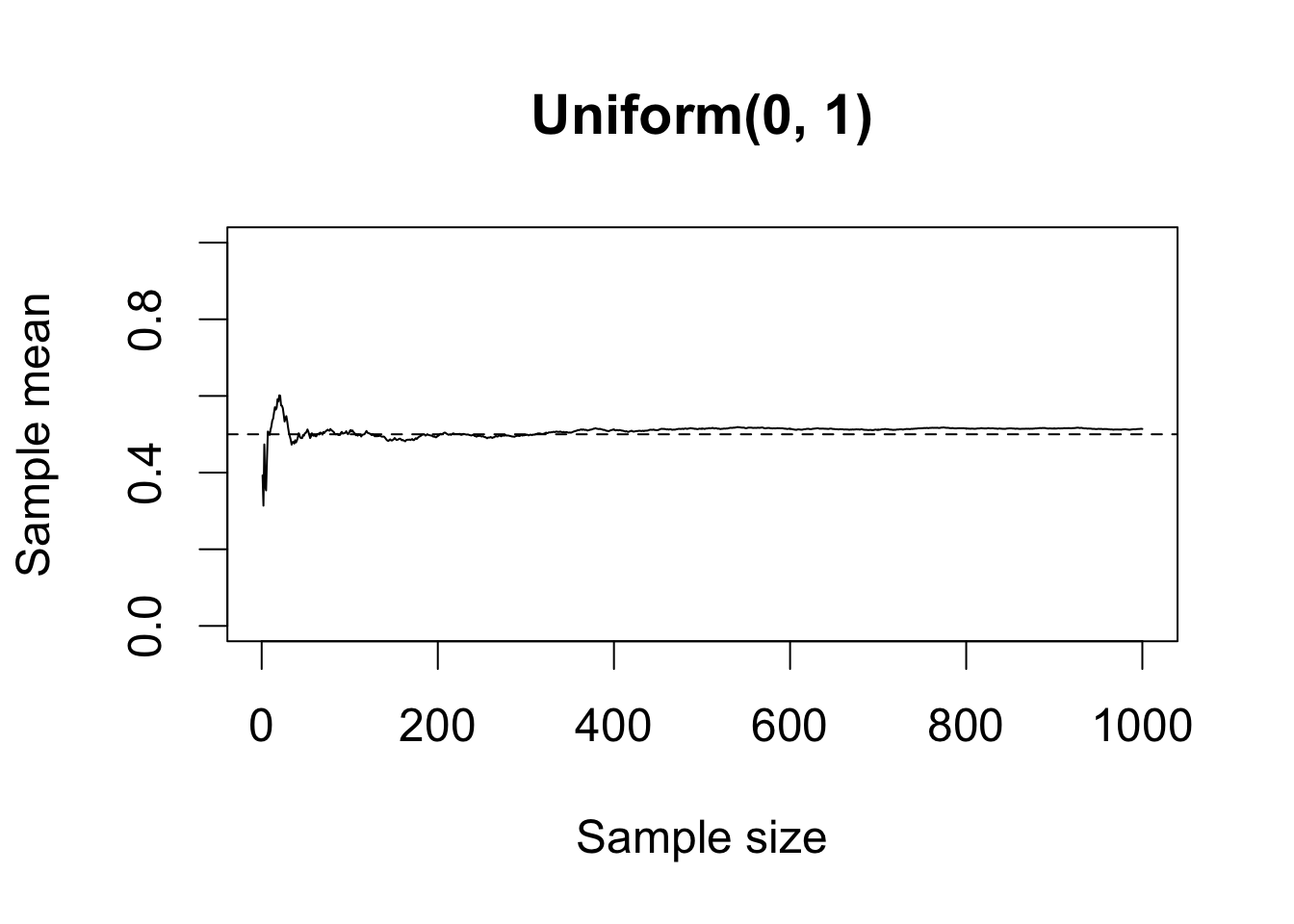
Section 6.2.1: Conditional, Marginal, and Joint Probabilities

data("FLVoters", package = "qss")
dim(FLVoters) # before removal of missing data

## [1] 10000     6

FLVoters <- na.omit(FLVoters)
dim(FLVoters) # after removal

## [1] 9113    6

margin.race <- prop.table(table(FLVoters$race))
margin.race

## 
##       asian       black    hispanic      native       other       white 
## 0.019203336 0.131021617 0.130802151 0.003182267 0.034017338 0.681773291

margin.gender <- prop.table(table(FLVoters$gender))
margin.gender

## 
##         f         m 
## 0.5358279 0.4641721

prop.table(table(FLVoters$race[FLVoters$gender == "f"]))

## 
##       asian       black    hispanic      native       other       white 
## 0.016997747 0.138849068 0.136391563 0.003481466 0.032357157 0.671922998

joint.p <- prop.table(table(race = FLVoters$race, gender = FLVoters$gender))
joint.p

##           gender
## race                 f           m
##   asian    0.009107868 0.010095468
##   black    0.074399210 0.056622408
##   hispanic 0.073082410 0.057719741
##   native   0.001865467 0.001316800
##   other    0.017337869 0.016679469
##   white    0.360035115 0.321738176

rowSums(joint.p)

##       asian       black    hispanic      native       other       white 
## 0.019203336 0.131021617 0.130802151 0.003182267 0.034017338 0.681773291

colSums(joint.p)

##         f         m 
## 0.5358279 0.4641721

FLVoters$age.group <- NA # initialize a variable
FLVoters$age.group[FLVoters$age <= 20] <- 1
FLVoters$age.group[FLVoters$age > 20 & FLVoters$age <= 40] <- 2
FLVoters$age.group[FLVoters$age > 40 & FLVoters$age <= 60] <- 3
FLVoters$age.group[FLVoters$age > 60] <- 4

joint3 <-
    prop.table(table(race = FLVoters$race, age.group = FLVoters$age.group,
                     gender = FLVoters$gender))
joint3

## , , gender = f
## 
##           age.group
## race                  1            2            3            4
##   asian    0.0001097333 0.0026336004 0.0041698672 0.0021946670
##   black    0.0016460002 0.0280917371 0.0257873368 0.0188741358
##   hispanic 0.0015362669 0.0260068035 0.0273236036 0.0182157358
##   native   0.0001097333 0.0004389334 0.0006584001 0.0006584001
##   other    0.0003292000 0.0062548008 0.0058158674 0.0049380007
##   white    0.0059256008 0.0796664106 0.1260836168 0.1483594864
## 
## , , gender = m
## 
##           age.group
## race                  1            2            3            4
##   asian    0.0002194667 0.0028530670 0.0051574674 0.0018654669
##   black    0.0016460002 0.0228245364 0.0189838692 0.0131680018
##   hispanic 0.0016460002 0.0197520026 0.0221661363 0.0141556019
##   native   0.0000000000 0.0004389334 0.0003292000 0.0005486667
##   other    0.0004389334 0.0069132009 0.0055964007 0.0037309338
##   white    0.0040601339 0.0750576100 0.1184022825 0.1242181499

## marginal probabilities for age groups
margin.age <- prop.table(table(FLVoters$age.group))
margin.age

## 
##          1          2          3          4 
## 0.01766707 0.27093164 0.36047405 0.35092725

## P(black and female | above 60)
joint3["black", 4, "f"] / margin.age[4]

##          4 
## 0.05378361

## two-way joint probability table for age group and gender
joint2 <- prop.table(table(age.group = FLVoters$age.group,
                           gender = FLVoters$gender))
joint2

##          gender
## age.group           f           m
##         1 0.009656535 0.008010534
##         2 0.143092286 0.127839350
##         3 0.189838692 0.170635356
##         4 0.193240426 0.157686821

joint2[4, "f"] # P(above 60 and female)

## [1] 0.1932404

## P(black | female and above 60)
joint3["black", 4, "f"] / joint2[4, "f"]

## [1] 0.09767178

Section 6.2.2: Independence

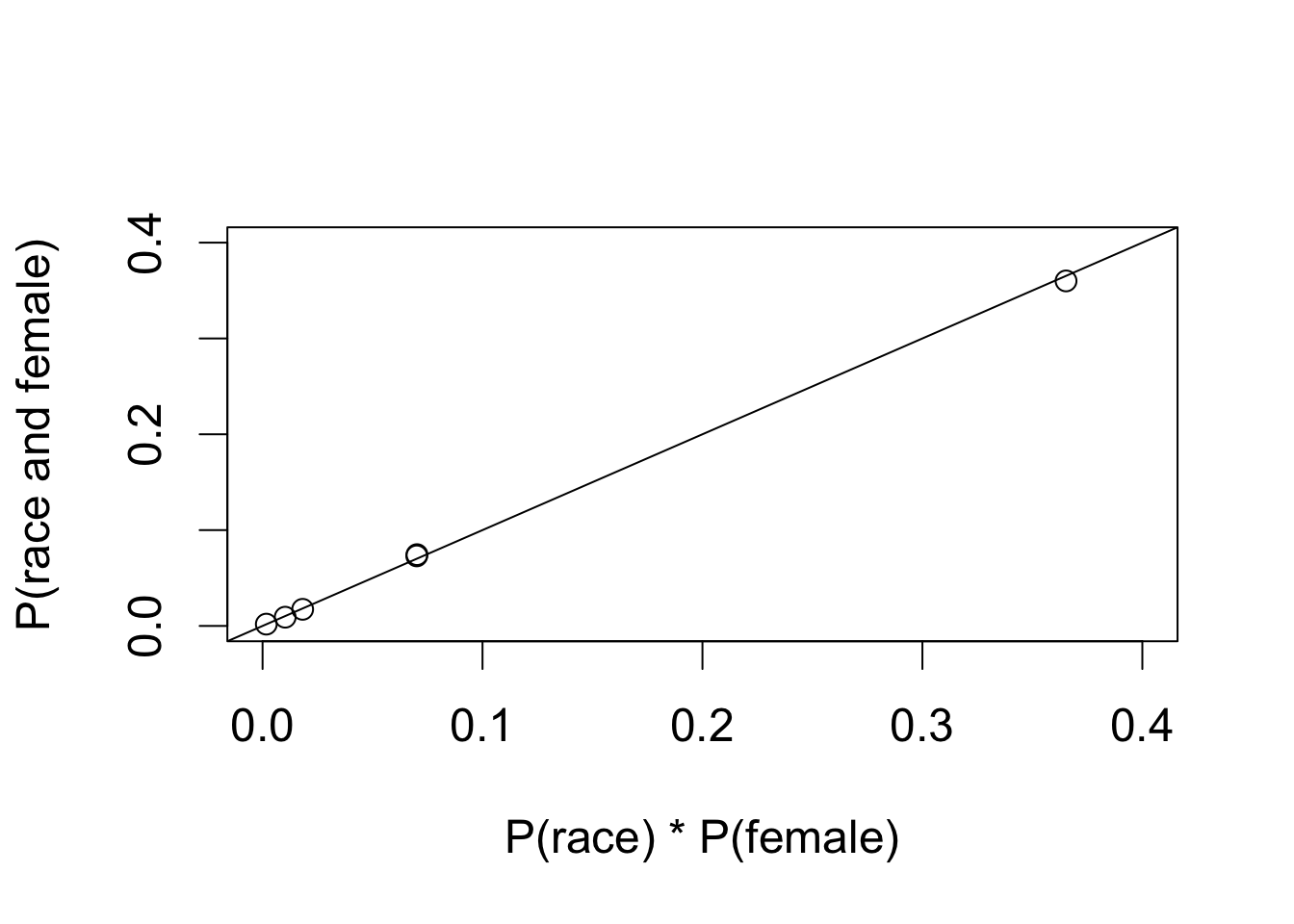
par(cex = 1.5)
plot(c(margin.race * margin.gender["f"]), # product of marginal probs.
     c(joint.p[, "f"]), # joint probabilities
     xlim = c(0, 0.4), ylim = c(0, 0.4),
     xlab = "P(race) * P(female)", ylab = "P(race and female)")
abline(0, 1) # 45 degree line

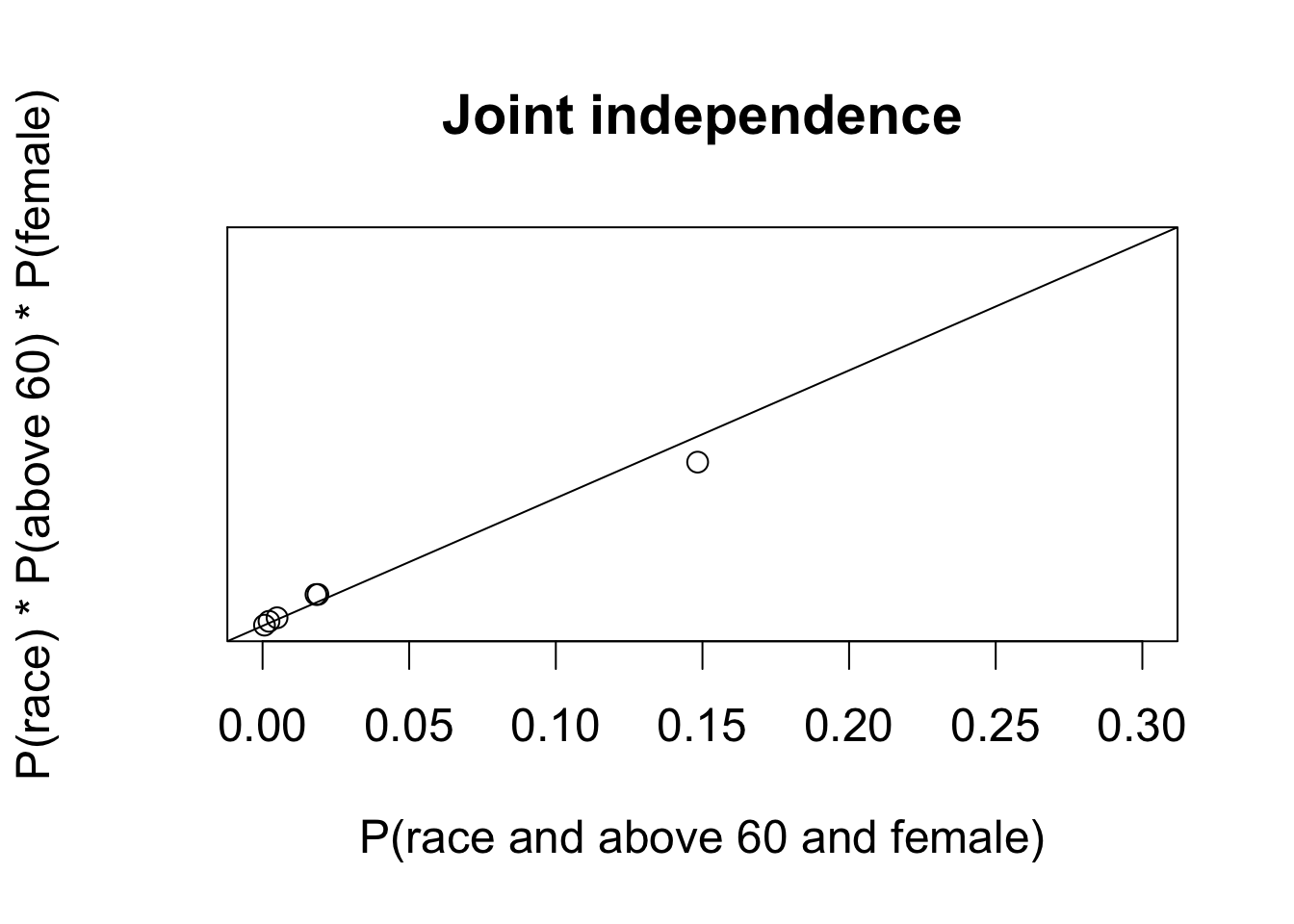
par(cex = 1.5)

## joint independence
plot(c(joint3[, 4, "f"]), # joint probability
     margin.race * margin.age[4] * margin.gender["f"], # product of marginals
     xlim = c(0, 0.3), ylim = c(0, 0.3), main = "Joint independence",
     xlab = "P(race and above 60 and female)",
     ylab = "P(race) * P(above 60) * P(female)")
abline(0, 1)

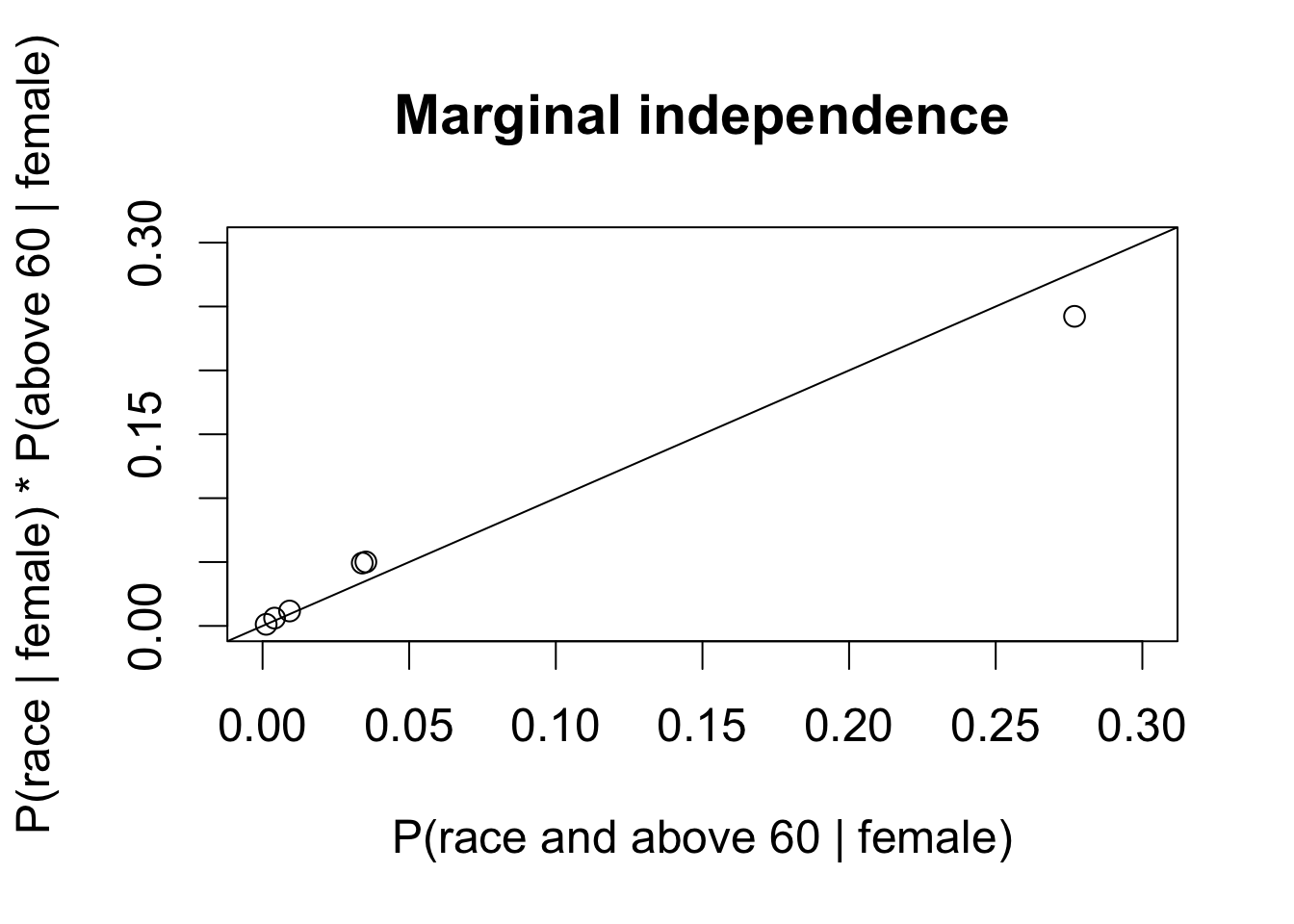
## conditional independence given female
plot(c(joint3[, 4, "f"]) / margin.gender["f"], # joint prob. given female
     ## product of marginals
     (joint.p[, "f"] / margin.gender["f"]) *
         (joint2[4, "f"] / margin.gender["f"]),
     xlim = c(0, 0.3), ylim = c(0, 0.3), main = "Marginal independence",
     xlab = "P(race and above 60 | female)",
     ylab = "P(race | female) * P(above 60 | female)")
abline(0, 1)

sims <- 1000
doors <- c("goat", "goat", "car")
result.switch <- result.noswitch <- rep(NA, sims)

for (i in 1:sims) {
    ## randomly choose the initial door
    first <- sample(1:3, size = 1)
    result.noswitch[i] <- doors[first]
    remain <- doors[-first] # remaining two doors
    ## Monty chooses one door with a goat
    monty <- sample((1:2)[remain == "goat"], size = 1)
    result.switch[i] <- remain[-monty]
}

mean(result.noswitch == "car")

## [1] 0.324

mean(result.switch == "car")

## [1] 0.676

Section 6.2.4: Predicting Race Using Surname and Residence Location

data("cnames", package = "qss")
dim(cnames)

## [1] 151671      7

x <- c("blue", "red", "yellow")
y <- c("orange", "blue")

## match x with y
match(x, y) # `blue' appears in the 2nd element of y

## [1]  2 NA NA

## match y with x
match(y, x) # `blue' appears in the 1st element of x

## [1] NA  1

FLVoters <- FLVoters[!is.na(match(FLVoters$surname, cnames$surname)), ]
dim(FLVoters)

## [1] 8022    7

whites <- subset(FLVoters, subset = (race == "white"))
w.indx <- match(whites$surname, cnames$surname)
head(w.indx)

## [1]  8610   237  4131  2244 27852  3495

## relevant variables
vars <- c("pctwhite", "pctblack", "pctapi", "pcthispanic", "pctothers")
mean(apply(cnames[w.indx, vars], 1, max) == cnames$pctwhite[w.indx])

## [1] 0.950218

## blacks
blacks <- subset(FLVoters, subset = (race == "black"))
b.indx <- match(blacks$surname, cnames$surname)

mean(apply(cnames[b.indx, vars], 1, max) == cnames$pctblack[b.indx])

## [1] 0.1604824

## Hispanics
hispanics <- subset(FLVoters, subset = (race == "hispanic"))
h.indx <- match(hispanics$surname, cnames$surname)

mean(apply(cnames[h.indx, vars], 1, max) == cnames$pcthispanic[h.indx])

## [1] 0.8465298

## Asians
asians <- subset(FLVoters, subset = (race == "asian"))
a.indx <- match(asians$surname, cnames$surname)

mean(apply(cnames[a.indx, vars], 1, max) == cnames$pctapi[a.indx])

## [1] 0.5642857

indx <- match(FLVoters$surname, cnames$surname)

## whites false discovery rate
1 - mean(FLVoters$race[apply(cnames[indx, vars], 1, max) ==
                           cnames$pctwhite[indx]] == "white")

## [1] 0.1973603

## black false discovery rate
1 - mean(FLVoters$race[apply(cnames[indx, vars], 1, max) ==
                           cnames$pctblack[indx]] == "black")

## [1] 0.3294574

## Hispanic false discovery rate
1 - mean(FLVoters$race[apply(cnames[indx, vars], 1, max) ==
                           cnames$pcthispanic[indx]] == "hispanic")

## [1] 0.2274755

## Asian false discovery rate
1 - mean(FLVoters$race[apply(cnames[indx, vars], 1, max) ==
                           cnames$pctapi[indx]] == "asian")

## [1] 0.3416667

data("FLCensus", package = "qss")

## compute proportions by applying weighted.mean() to each column
race.prop <-
    apply(FLCensus[, c("white", "black", "api", "hispanic", "others")],
          2, weighted.mean, weights = FLCensus$total.pop)

race.prop # race proportions in Florida

##      white      black        api   hispanic     others 
## 0.60451586 0.13941679 0.02186662 0.21279972 0.02140101

total.count <- sum(cnames$count)

## P(surname | race) = P(race | surname) * P(surname) / P(race)
cnames$name.white <- (cnames$pctwhite / 100) *
    (cnames$count / total.count) / race.prop["white"]

cnames$name.black <- (cnames$pctblack / 100) *
    (cnames$count / total.count) / race.prop["black"]

cnames$name.hispanic <- (cnames$pcthispanic / 100) *
    (cnames$count / total.count) / race.prop["hispanic"]

cnames$name.asian <- (cnames$pctapi / 100) *
    (cnames$count / total.count) / race.prop["api"]

cnames$name.others <- (cnames$pctothers / 100) *
    (cnames$count / total.count) / race.prop["others"]

FLVoters <- merge(x = FLVoters, y = FLCensus, by = c("county", "VTD"),
                  all = FALSE)

## P(surname | residence) = sum_race P(surname | race) P(race | residence)
indx <- match(FLVoters$surname, cnames$surname)

FLVoters$name.residence <- cnames$name.white[indx] * FLVoters$white +
    cnames$name.black[indx] * FLVoters$black +
    cnames$name.hispanic[indx] * FLVoters$hispanic +
    cnames$name.asian[indx] * FLVoters$api +
    cnames$name.others[indx] * FLVoters$others

## P(race | surname, residence) = P(surname | race) * P(race | residence)
##                                / P(surname | residence)
FLVoters$pre.white <- cnames$name.white[indx] * FLVoters$white /
    FLVoters$name.residence

FLVoters$pre.black <- cnames$name.black[indx] * FLVoters$black /
    FLVoters$name.residence

FLVoters$pre.hispanic <- cnames$name.hispanic[indx] * FLVoters$hispanic /
    FLVoters$name.residence

FLVoters$pre.asian <- cnames$name.asian[indx] * FLVoters$api /
    FLVoters$name.residence

FLVoters$pre.others <- 1 - FLVoters$pre.white - FLVoters$pre.black -
    FLVoters$pre.hispanic - FLVoters$pre.asian

## relevant variables
vars1 <- c("pre.white", "pre.black", "pre.hispanic", "pre.asian",
           "pre.others")
## whites
whites <- subset(FLVoters, subset = (race == "white"))
mean(apply(whites[, vars1], 1, max) == whites$pre.white)

## [1] 0.9371366

## blacks
blacks <- subset(FLVoters, subset = (race == "black"))
mean(apply(blacks[, vars1], 1, max) == blacks$pre.black)

## [1] 0.6474954

## Hispanics
hispanics <- subset(FLVoters, subset = (race == "hispanic"))
mean(apply(hispanics[, vars1], 1, max) == hispanics$pre.hispanic)

## [1] 0.85826

## Asians
asians <- subset(FLVoters, subset = (race == "asian"))
mean(apply(asians[, vars1], 1, max) == asians$pre.asian)

## [1] 0.6071429

## proportion of blacks among those with surname "White"
cnames$pctblack[cnames$surname == "WHITE"]

## [1] 27.38

## predicted probability of being black given residence location
summary(FLVoters$pre.black[FLVoters$surname == "WHITE"])

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## 0.005207 0.081154 0.176265 0.264042 0.320035 0.983717

## whites
1 - mean(FLVoters$race[apply(FLVoters[, vars1], 1, max) ==
                           FLVoters$pre.white] == "white")

## [1] 0.1187425

## blacks
1 - mean(FLVoters$race[apply(FLVoters[, vars1], 1, max) ==
                           FLVoters$pre.black] == "black")

## [1] 0.2346491

## Hispanics
1 - mean(FLVoters$race[apply(FLVoters[, vars1], 1, max) ==
                           FLVoters$pre.hispanic] == "hispanic")

## [1] 0.2153709

## Asians
1 - mean(FLVoters$race[apply(FLVoters[, vars1], 1, max) ==
                           FLVoters$pre.asian] == "asian")

## [1] 0.3461538

Section 6.3: Random Variables and Probability Distributions

Section 6.3.1: Random Variables

Section 6.3.2: Bernoulli and Uniform Distributions

## uniform PDF: x = 0.5, interval = [0, 1]
dunif(0.5, min = 0, max = 1)

## [1] 1

## uniform CDF: x = 1, interval = [-2, 2]
punif(1, min = -2, max = 2)

## [1] 0.75

sims <- 1000
p <- 0.5 # success probabilities
x <- runif(sims, min = 0, max = 1) # uniform [0, 1]
head(x)

## [1] 0.5678733 0.9410816 0.5185468 0.1238836 0.8536242 0.9228207

y <- as.integer(x <= p) # Bernoulli; turn TRUE/FALSE to 1/0
head(y)

## [1] 0 0 0 1 0 0

mean(y) # close to success probability p, proportion of 1's vs. 0's

## [1] 0.503

Section 6.3.3: Binomial Distribution

## PMF when x = 2, n = 3, p = 0.5
dbinom(2, size = 3, prob = 0.5)

## [1] 0.375

## CDF when x = 1, n = 3, p = 0.5
pbinom(1, size = 3, prob = 0.5)

## [1] 0.5

## number of voters who turn out
voters <- c(1000, 10000, 100000)
dbinom(voters / 2, size = voters, prob = 0.5)

## [1] 0.025225018 0.007978646 0.002523126

Section 6.3.4: Normal Distribution

## plus minus one standard deviation from the mean
pnorm(1) - pnorm(-1)

## plus minus two standard deviations from the mean
pnorm(2) - pnorm(-2)

mu <- 5
sigma <- 2

## plus minus one standard deviation from the mean
pnorm(mu + sigma, mean = 5, sd = 2) - pnorm(mu - sigma, mean = 5, sd = 2)

## plus minus two standard deviations from the mean
pnorm(mu + 2*sigma, mean = 5, sd = 2) - pnorm(mu - 2*sigma, mean = 5, sd = 2)

## see the page reference above
## `Obama2012.z' is Obama's 2012 standardized vote share
## `Obama2008.z' is Obama's 2008 standardized vote share
fit1

par(cex = 1.5)
e <- resid(fit1)

## z-score of residuals
e.zscore <- scale(e)

## alternatively we can divide residuals by their standard deviation
e.zscore <- e / sd(e)

hist(e.zscore, freq = FALSE, ylim = c(0, 0.4),
     xlab = "Standardized residuals",
     main = "Distribution of standardized residuals")

x <- seq(from = -3, to = 3, by = 0.01)
lines(x, dnorm(x)) # overlay the Normal density
qqnorm(e.zscore, xlim = c(-3, 3), ylim = c(-3, 3)) # quantile-quantile plot

abline(0, 1) # 45 degree line

e.sd <- sd(e)
e.sd

CA.2008 <- pres$Obama2008.z[pres$state == "CA"]
CA.2008

CA.mean2012 <- coef(fit1) * CA.2008
CA.mean2012

## area to the right; greater than CA.2008
pnorm(CA.2008, mean = CA.mean2012, sd = e.sd, lower.tail = FALSE)

TX.2008 <- pres$Obama2008.z[pres$state == "TX"]
TX.mean2012 <- coef(fit1) * TX.2008
TX.mean2012

pnorm(TX.2008, mean = TX.mean2012, sd = e.sd, lower.tail = FALSE)

Section 6.3.5: Expectation and Variance

## theoretical variance: p was set to 0.5 earlier
p * (1-p)

## [1] 0.25

## sample variance using `y' generated earlier
var(y)

## [1] 0.2502412

Section 6.3.6: Predicting Election Outcomes with Uncertainty

data("pres08", package = "qss")

## two-party vote share
pres08$p <- pres08$Obama / (pres08$Obama + pres08$McCain)

par(cex = 1.5)
n.states <- nrow(pres08) # number of states
n <- 1000 # number of respondents
sims <- 10000 # number of simulations

## Obama's electoral votes
Obama.ev <- rep(NA, sims)

for (i in 1:sims) {
    ## samples number of votes for Obama in each state
    draws <- rbinom(n.states, size = n, prob = pres08$p)
    ## sums state's electoral college votes if Obama wins the majority
    Obama.ev[i] <- sum(pres08$EV[draws > n / 2])
}

hist(Obama.ev, freq = FALSE, main = "Prediction of election outcome",
     xlab = "Obama's electoral college votes")
abline(v = 364, col = "red") # actual result

summary(Obama.ev)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   289.0   341.0   353.0   352.3   364.0   409.0

mean(Obama.ev)

## [1] 352.322

## probability of binomial random variable taking greater than n/2 votes
sum(pres08$EV * pbinom(n / 2, size = n, prob = pres08$p, lower.tail = FALSE))

## [1] 352.1388

## approximate variance using Monte Carlo draws
var(Obama.ev)

## [1] 267.5675

## theoretical variance
pres08$pb <- pbinom(n / 2, size = n, prob = pres08$p, lower.tail = FALSE)
V <- sum(pres08$pb * (1 - pres08$pb) * pres08$EV^2)
V

## [1] 268.8008

## approximate standard deviation using Monte Carlo draws
sd(Obama.ev)

## [1] 16.35749

## theoretical standard deviation
sqrt(V)

## [1] 16.39515

Section 6.4: Large Sample Theorems

Section 6.4.1: The Law of Large Numbers

sims <- 1000

## 3 separate simulations for each
x.binom <- rbinom(sims, p = 0.2, size = 10)

## computing sample mean with varying sample size
mean.binom <- cumsum(x.binom) / 1:sims

## default runif() is uniform(0, 1)
x.unif <- runif(sims)
mean.unif <- cumsum(x.unif) / 1:sims

par(cex = 1.5)
## plot for binomial
plot(1:sims, mean.binom, type = "l", ylim = c(1, 3),
     xlab = "Sample size", ylab = "Sample mean", main = "Binomial(10, 0.2)")
abline(h = 2, lty = "dashed") # expectation

## plot for uniform
plot(1:sims, mean.unif, type = "l", ylim = c(0, 1),
     xlab = "Sample size", ylab = "Sample mean", main = "Uniform(0, 1)")
abline(h = 0.5, lty = "dashed") # expectation

Section 6.4.2: The Central Limit Theorem

par(cex = 1.5)
## sims = number of simulations
n.samp <- 1000
z.binom <- z.unif <- rep(NA, sims)

for (i in 1:sims) {
    x <- rbinom(n.samp, p = 0.2, size = 10)
    z.binom[i] <- (mean(x) - 2) / sqrt(1.6 / n.samp)
    x <- runif(n.samp, min = 0, max = 1)
    z.unif[i] <- (mean(x) - 0.5) / sqrt(1 / (12 * n.samp))
}

## histograms; nclass specifies the number of bins
hist(z.binom, freq = FALSE, nclass = 40, xlim = c(-4, 4), ylim = c(0, 0.6),
     xlab = "z-score", main = "Binomial(0.2, 10)")

x <- seq(from = -3, to = 3, by = 0.01)
lines(x, dnorm(x)) # overlay the standard Normal PDF

hist(z.unif, freq = FALSE, nclass = 40, xlim = c(-4, 4), ylim = c(0, 0.6),
     xlab = "z-score", main = "Uniform(0, 1)")
lines(x, dnorm(x))

Section 6.5: Summary